For the past year at MOTH we have been working a lot with quantum reservoir computing (QRC for short). This is a new kind of software designed to run on quantum computers. We’ve applied it both to music and to games, culminating in our upcoming launch of a live game with on-demand quantum generation at Gamescom this year.
In this blog post we won’t describe the technical details of QRC. For that you can check out our papers, such as this one. Instead we are going to talk about some examples of it in use. Specifically, we’ll briefly touch on how to use it for game level generation, and then focus on how to use it for game music too.
QRC for game levels
The job of QRC is to look at and learn sequences of data. Then, when given new sequences, it has to predict the next element. This makes it potentially useful for applications such as forecasting the weather or even financial events. It also means that it can be used as a generative technology. We can take content that can be expressed as a sequence, such as music or certain game levels, and then riff on that content to generate new things.
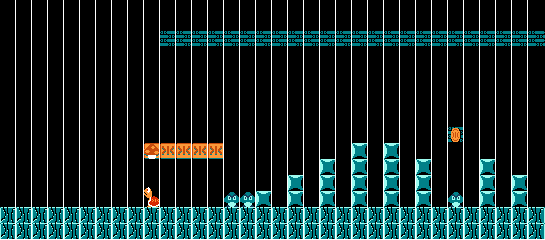
Let’s start with game levels. Specifically, let’s take the second level of Super Mario Bros.
To understand how we can treat this as a sequence, let’s take a closer look at the beginning.
As you’ll probably notice, here we added a vertical white line every 16 pixels. With this we can see that the level is made up of a sequence of repeating features. It starts with just the empty floor (let’s call it feature 0). Then, after repeating this nine times, we move on to a Koopa and a mushroom (feature 1). Then there are four question mark blocks (feature 2), followed by a couple of Goombas (feature 3). If we continue in this way, we can convert the level into a sequence of integers:
0,0,0,0,0,0,0,0,0,1,2,2,2,2,3,3,4,5,6,5,7,5,8,5,8,5,7,5,9,5,7,5,6,5,...It’s not as pretty in this form, but it is now something we can feed into our QRC system to create new and remixed versions of this Mario level.
Music for Mario
Suppose a future archeologist found the above sequence of integers with no context whatsoever. What might they think it is? Probably they wouldn’t guess that it is a description of an underground world to be traversed by a plumber.
Perhaps they might guess that it was music. It starts with repetition and then kicks off with an alternation between repetition and an ascending sequence. Of course the archeologist wouldn’t know exactly which notes or musical motifs are described by each number. But if they were sufficiently musically motivated, perhaps they’d even try to compose new music for this unknown score.
This is exactly the task given to Dr Rakhat-Bi Abdyssagin, avant-garde composer, concert pianist, music theorist, and MOTH researcher. Given the full sequence of this Mario level, a list of 157 numbers each between 0 and 31, his job was to compose a musical motif for each.
In this composition he looked at the way each feature appears in the level, and the way they interplay with other features in the sequence. Feature 0 needs to be one that can be repeated 9 times in a row, for example. Feature 5 should be one that works well with 4, 6, 7 and 8, and the ascending and descending of 4, 6, 7 and 8 should create an impact.
In his own words:
Each bar has a duration of one beat (1/4) and represents a certain number. The score was written in ‘one line’ so that it can be performed by a great variety of different instruments, and the range was chosen in such a way that it will make the score versatile and able to fit the actual ranges of multiple instruments. To give a sense of uniqueness to each number/bar, a number of approaches were used to create symmetrical structures in the score, for example, in some places making even numbers ‘go up’ and odd numbers ‘go down’. Though this is a ‘monophonic’ piece, certain polyphonical techniques were used, including isorhythm, interpolation, polarisation, retrogrades, inversions, and many other operations possible with a tone row, etc. A challenge while composing the score was to make each bar (number) to be self-sufficient, with inner dramaturgy and form, so that any combination of bars/numbers will sound in a coherent and structurally aligned way. Any bar can be a beginning or a continuation of another one, and any imaginable structure is permitted. This allows the creation of enormously large possible variations based on the existing bars/numbers. The self-sufficiency yet complementarity of every single bar maintains the combinatorial architectonics of the entire composition. The numbers (allowing repetitions etc.) can be (re-)arranged in any thinkable and unthinkable way, and so is the music (the bars). This is a ‘controlled’ randomness, an order that evolves from chaos, or the chaos as the highest state of order. The sequence of numbers/bars will be generated each time anew by quantum computing, thus every time there will be ’new’ music, which will still be the same composition. This is metaphorically like topological changes of shape while maintaining the ‘essence’.
Before listening to the full piece, let’s first just focus on this segment.
Despite having possibly never played Mario in his life (despite a vague memory in which he remembers a lot of jumping), Rakhat-Bi somehow nailed the Mario sound with this bit.
Now for the full piece, this time on piano.
Now we have turned a Mario level into a piece of music, let’s see what QRC does to it. When we use QRC to generate new levels, it will reproduce some of the structure of the original level, as well as adding in something new. The musical choices made for the original level should then translate to good music for any remixed ones.
To see this in action, let’s take some results that we obtained from a real QPU, namely IQM’s Garnet device. Here’s what these results look like as a Mario level.
And here’s what they sound like with Rakhat-Bi’s score.
Music for Moths
Now it’s time to make a game of our own. Using this same principle as before we made a new game: Space Moths. This is a Roblox race game in which the course can similarly be represented as a sequence of numbers, allowing us to generate courses on-demand with our QRC system.
This game needs music. And since music can be remixed with QRC, we need to do that too. We could achieve this by first composing some music, then expressing it as a sequence of numbers, and then using QRC to infinitely remix it. Indeed that’s exactly what we did in a previous project, collaborating with the artist ILĀ to create a new single and an infinite remix of it.
However, bear in mind that we are also using QRC to generate the levels. Using it for the music as well would meanrunning both processes at the same time. Since we are running our QRC on quantum computers, which as an emerging technology is not the world’s most abundant resource, this is not something we want to do. So instead we’ll use the approach of the previous section: we’ll only generate levels using QRC, and then turn those into the in-game music.
Space Moths is a racing game in which you fly through and past a mix of obstacles. It is this sequence of obstacles that is represented by the sequence of numbers. For example, feature 15 has you dodging asteroids while feature 11 has you dodging debris.
As in the Mario level, the features in the levels are not just arranged randomly. Instead they are grouped in a way that makes sense narratively. For example, the asteroids and debris always occur near each other, because the asteroid strikes are what cause the debris. They shouldn’t occur anywhere near nicely ordered obstacles like 22 and 23 below, which will instead be part of sequences which involve a lot of flying through holes.
But enough about the game. Now let’s turn these sequences into music! This time the task was given to MOTH predoctoral researcher Alex Alani.
Given the 32 possible integers in the levels, he interprets each as a small chunk of music consisting of 2 bars of 4/4 time. This means 8 beats, and therefore 4 seconds at 120 bpm. When composing for the structure of the level, to keep the composition diatonic (pleasant sounding), he kept each integer in the same key for the purpose of cohesion.
As Alex says:
Within the context of Space Moths specifically, each integer is 2 bars of 4/4 time outlining a back door progression of a bVI, bVII, I, V progression where each roman numeral is two beats given the overall key resolves to C Major as the I.
Given these principles, here are some examples of what he composed. Specifically, here’s the music corresponding to 11 and 15.
And here are 22 and 23.
As millennial readers might notice, we are going for an F-Zero kinda vibe here.
Here’s Alex’s explanation of how he chose to compose these segments.
Because the music corresponding to integer 11 is the debris field and the music corresponding to integer 15 is the asteroid belt, musically I used a type of a distortion to represent these wreckage vibes. The distortion I used is relevant to my PhD research in Quantum Computer Music at the University of Plymouth because it is a Simulated Quantum Gate Distortion (SQGD) where using Moth’s Quantum Audio Python package, I map digital audio’s time to quantum states on a simulated quantum computer where quantum gates are added to create various forms of distortion.
Since integer 22 is the spinner maze and integer 23 is the narrow tunnel flicker, these are not wreckage like integers 11 and 15 so they do not use the SQGD. So basically, not only is there music relevance to the quantum computing concepts of QRC that generate the sequences of each video game level, but within the soundtrack of Space Moths there are applications of Moth’s quantum audio research.
Finally, here is the whole piece as a musical form of a Space Moths level.
If you want to hear remixes of this track using QRC running on real quantum hardware, then all you need to do is get onto Roblox and search for Space Moths once it is released in the week of 18th August. We’ll see you in there!